judy 发布于：周二, 08/08/2017 - 15:00 ，关键词：

• C2000
• 浮点数

C28x+FPU架构的C2000微处理器在原有的C28x定点CPU的基础上加入了一些寄存器和指令，来支持IEEE 单精度浮点数的运算。对于在定点微处理器上编写的程序，浮点C2000也完全兼容，不需要对程序做出改动。浮点处理器相对于定点处理器有如下好处：

1.编程更简单
2.性能更优，比如除法，开方，FFT和IIR滤波等算法运算效率更高。
3.程序鲁棒性更强。

一、IEEE754格式的浮点数
C28x+FPU的单精度浮点数遵循IEEE754格式。它包括：
- 1位符号位：0表示正数，1表示负数。
- 8位阶码
- 23位尾数

表1：IEEE单精度浮点数

(1)非规格化数值非常小，计算公式为(-1)sx2(E-126)x0.M
(2)正常范围数值计算公式为(-1)sx2(E-127)x1.M

正常范围数值落在± ~1.7 x 10 -38 to ± ~3.4 x 10 +38范围内。从表1可以看出，IEEE754标准包括：
- 标准数据格式和特殊值，比如非数值(NaN)和无穷大
- 标准舍入模式和浮点运算
- 多平台支持，包括德州仪器C67x系列芯片。

C2000对该标准作了一些简化：
- 状态标志位和比较运算不区分正0和负0
- 非规格化数值被认为是0
- 对非数值(NaN)处理方式和无穷大一样。

IEEE754标准有5种舍入模式，C28x+FPU只支持其中两种：
--截断：小数位不管大小全部舍去
--就近舍入向偶舍入：这种模式下如果小数位小于5就舍去，大于5就进位，如果小数位为5，则舍入到最近的偶数。
表2展示了不同的舍入模式对数据的影响。C28x+FPU编译器默认将微处理器配置为就近舍入向偶舍入模式[1]。

二、浮点C2000芯片运算技巧和注意点

浮点数的精度由尾数位决定，绝大多数的数在用浮点数表示时都会有误差，这些误差很小，多数情况下可以忽略，但是在经过多次计算后这个误差可能会大到无法接受。

下面用实例来进行说明，下面一段代码定义float类型变量，分别在TI最新的Delfino芯片F28379D的CPU1和CLA1上，将11.7加20001次。
float CLATMPDATA=0;
int index=20001;
while(index--)
{
CLATMPDATA=CLATMPDATA+11.7;
}
得到如下结果：

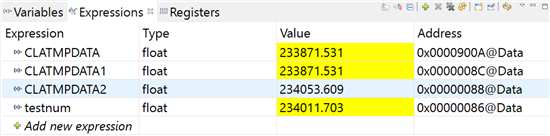
其中CLATMPDATA1是在CLA中将11.7加20001次得到的结果，CLATMPDATA2是在CPU中将11.7加20001次得到的结果。可以看出两者所得到的结果不同，并且都和正确结果234011.7有较大差距。

1.为何CPU和CLA计算结果不同？

CPU和CLA运算结果的不同是由于其对浮点数的舍入模式的不同造成的，前文已经说过，C28x+FPU 编译器默认将CPU配置为就近舍入向偶舍入模式。而CLA不同，CLA默认为截断舍入模式[2]。在CLA的代码中，我们可以通过增加下述代码：

__asm(" MSETFLG RNDF32=1");//1为就近舍入向偶舍入，0为截断舍入
将CLA的舍入模式更改为就近舍入向偶舍入模式，然后再运行代码，可以得到和CPU同样的结果。

11.7在用IEEE754格式的浮点数表示时为0x413b3333，其对应的实际值为11.69999980926513671875，可以看出误差很小，但是经过多次累加多次舍入后得到的结果误差较大，对此，我们可以将CLATMPDATA定义为long double型变量（64位），再次运行相同的代码，可以得到如下结果，可以看到误差很小可以忽略。

在这个实例中，我们可以分别观察float类型变量和long double类型变量的汇编代码如下：
C code: CLATMPDATA2=CLATMPDATA2+11.7;

如果CLATMPDATA2是float型变量，则相应的汇编代码为：
00c08d: E80209D8 MOVIZ R0, #0x413b 1cycle
00c08f: E2AF0112 MOV32 R1H, @0x12, UNCF 1cycle
00c091: E8099998 MOVXI R0H, #0x3333 1cycle
00c093: E7100040 ADDF32 R0H, R0H, R1H 2cycle
00c095: 7700 NOP 1cycle
00c096: E2030012 MOV32 @0x12, R0H 1cycle

如果CLATMPDATA2是long double型变量，则相应的汇编代码为：
00c08b: 7680005A MOVL XAR6, #0x00005a 1cycle
00c08d: 8F00005A MOVL XAR4, #0x00005a 1cycle
00c08f: 8F40C26A MOVL XAR5, #0x00c26a 1cycle
00c091: FF69 SPM #0 1cycle
00c092: 7640C0C9 LCR FD$$ADD 4cycle（跳转耗时）
+25cycle（FD$$ADD函数内部需要25cycle）

可以看出CPU对float类型数执行一次加法耗时7个cycle，对long double类型数执行一次加法耗时33个cycle。

三、结论

1.C2000的CPU和CLA默认的舍入模式不同，在计算浮点数时可能会得到不同的结果，但是我们可以通过代码改变其舍入模式得到相同的结果。

2. 单精度浮点数经过多次计算后可能会有较大误差，可以通过将变量定义为64位long double型解决精度问题。

3. C28x CPU只支持单精度（32位）的硬件浮点运算，对于64位双精度浮点数的运算都是通过软件实现的，所以其运算速率会慢很多。在下一代的C2000产品中我们会实现对64位双精度浮点数运算的硬件支持。